CLOUDES is an ongoing STEM research effort, led by researchers at the Virginia Modeling, Analysis and Simulation Center at Old Dominion University, focused on making simulations accessible to anyone.

As such, we expect students, from middle to graduate schools, to benefit the most as they will have access to an intuitive simulation environment that focuses on the modeling process (moving from observation, to conceptual model, to simulation model  and ending with analysis of results). These capabilities are available through a browser across computing platforms with no need for writing code.

To maximize student outreach, we encourage educators to use CLOUDES in the classroom. We have found the ability to document models, share them and reuse them very useful in our teaching activities. In our testing/teaching sessions, students of all ages have found the environment easy to use when focusing on learning how to model not on learning the tool.

The CLOUDES Manual, and the available short videos, is a good starting point as it focuses on the modeling process aided by the environment. Should you have questions or comments please send us a note to cloudes@odu.edu.

• Revamped user interface: we are constantly looking for ways to make CLOUDES easier to use. A simple and intuitive interface is part of these efforts. We reduced the number of buttons (and added a new design) so you can access what you need faster. Settings and Replications can now be found under the Simulation Builder tab.
• Conceptual Design Module: This is perhaps the largest update. We have been testing this module for the last months and we feel confident you will find it useful. The module allows you to create a conceptual model and then convert it to a simulation model with a push of a button. The model is created with only one node that can later take the form of any node in the simulation model. Further details on how to use it will be provided in the blog (soon).
• Turkish is Available in the Design Area: You can access this option under your Profile. CLOUDES Design Area is now available in English, Spanish and Turkish. More language options will become available soon. We hope this change makes simulation use and creation accessible to more users worldwide.
• Documentation Upload: Under Settings, you can now upload a pdf document of your work. This allows you to keep track of your work and to facilitate others the replication of your public models.
• Description Nodes: To further facilitate your documentation, you can add as many Detailed Description nodes as needed on both the Conceptual Design and Simulation Builder modules.
• Automatic Counter and Schedules Import: When you import a model, any counter and schedule associated with it will be saved in your account.

Scheduling allows you to alter your resources (capacity) and inter-arrival time in Arrivals (the parameter for Poisson and Exponential distributions at the moment) for specific time intervals. As such, you would be able to model realistic time-dependent situations like rush hour, when arrival of customers increase during lunch time, or “slow times” like a reduction of cars in a toll booth during the hours of 9 pm and 5 am. This feature would allow the modeler to study the dynamics of the system during low and high traffic and establish how to allocate resources.

How to Use it.

A schedule depends on the time unit and simulation length of the simulation (see the environment tab). If the time unit is in minutes, then the schedule is in minutes. Likewise for days, hours and seconds. Considering simulation length, the modeler needs to assess what would be the period or periods where capacity and mean will change within the full timeframe. For instance, Schedule 2 in the figure below shows that within a day (1440 minutes) there will be three values for capacity: the one already assigned will go for the first 8 hours (479 minutes), a capacity of 1 will go for the following 8 hours and a capacity of 2 will go for the last 8 hours of the day.

The repeat option works by taking the full span of your schedule and repeats based on that.  For instance, if we run the simulation for two days (2880 minutes) and don’t want to enter values for the following day in the schedule, the repeat option would use the same values after adding the time interval: it will assign 1 at 1920 and 2 at 2400 until it finishes. Note the default capacity specified in the resource node is used from 0 to 479 minutes, and on repeat, the default will again be applied from 1441 to 1920 minutes. If you wish to use a value other than the default value during those times, a schedule like the one below would need to be used.

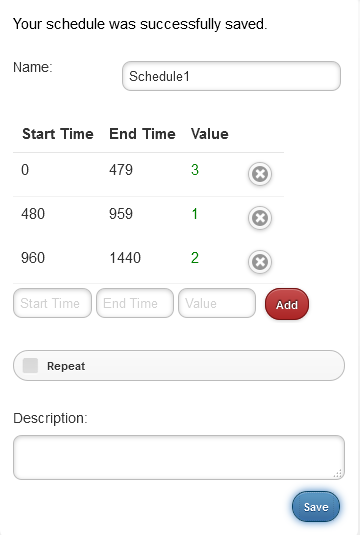
In this case (schedule1), if the repeat option is used the capacity of 3 will be assigned from 1441 until 1920; capacity of 1 from 1921 until 2400 and capacity of 2 from 2401 until 2880.

The same schedule can be applied to generate inter-arrival time in the Arrival block. As previously mentioned, it works for Poisson and Exponential distributions so far. It is noted that when applying a schedule to an inter-arrival distribution, a value of 0 in the schedule will stop the arrivals. The arrivals will remain stopped until a simulation time is reached in which the scheduled value is greater than zero.

Lastly, the resource block restricts capacity values to integers. However, the schedule permits decimal values. If a schedule which contains decimal values is applied to a resource, those decimal values will automatically be rounded to the nearest integer value during the build of the simulation. If the same schedule is also applied to an inter-arrival distribution, those decimal values will remain unchanged.

If you are planning on making your simulation Public, make sure you provide details. This way, other users can understand the system you attempt to represent, question you are trying to answer using the simulation, assumptions made, expected outcomes and insights you gained. It would help you make explicit your thoughts and mental models. Further, it would help other users reuse your simulations.

Use the Detailed Description under Environment to do so.

In addition to sample simulations, you can now find exercises with descriptions and with diagrams for you to practice! Make sure you read the Detailed Description Section under Environment.

CLOUDES has been going through many updates lately. Most of these updates are performance enhancements.  These enhancements improve loading times, tablet accessibility, and simulation import among others.

There are two major updates:

1. The first one focuses on capturing data for research purposes. While opening an account you will be asked if you want to participate in this effort. It is voluntary and it does not limit your creation of an account. If you already have an account, you can opt in through your profile page. We hope this data will provide insight into how to improve CLOUDES and how to design simulation learning strategies.

2. The second update gives users the option of having the simulation environment in Spanish. The interface, error messages, profile page, and simulation blocks among others change to Spanish by adjusting “Language” on your profile page. The main/landing page is still in English but we hope we can provide the Spanish version soon. We hope that this little change make simulation use and building accessible to more users worldwide.

• Fixed minor bugs
• Provided links to the user manual and to the blog from the main page. We hope that you take advantage of both.
• The blog will be updated frequently so you have new material to play with.
• Last, but not least we have a new logo that emphasizes our goal of putting YOU in the center of our efforts.